首页 算法相关
文章
取消

算法相关

发表于 2022/07/20 更新于 2022/12/18
作者
18 分钟阅读

时间复杂度

时间复杂度主要就是看基本操作是啥，然后基本操作要进行几次

O1

1
2
3
4
5

int i = 1;
int j = 2;
++i;
j++;
int m = i + j;

这代码操作都是执行一次。

On

1
2
3
4
5

for(i=1; i<=n; ++i)
{
   j = i;
   j++;
}

我们能看到，for循环的代码会执行n次。所以消耗的时间是随着n变化而变化。所以是On

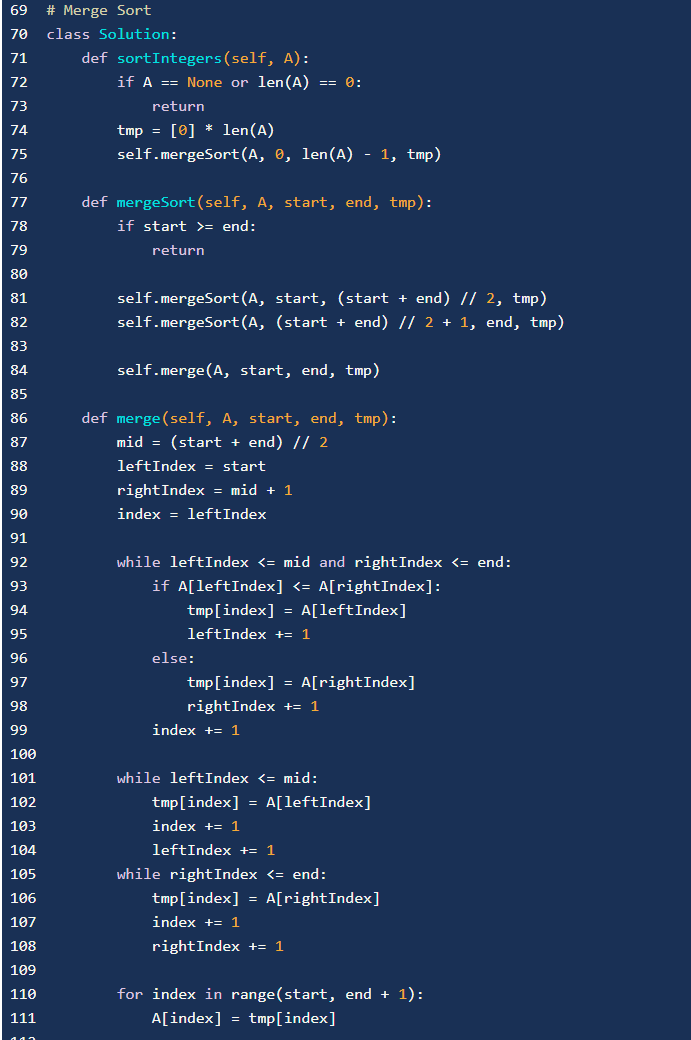
二叉树的遍历就是On，因为每个节点访问一次

O logN

1
2
3
4
5

int i = 1;
while(i<n)
{
    i = i * 2;
}

我们看到，while循环的i虽然随着n变化而变化，但是每次i是指数增长。所以复杂度也就是对数。

O NlogN

1
2
3
4
5
6
7
8

for(m=1; m<n; m++)
{
    i = 1;
    while(i<n)
    {
        i = i * 2;
    }
}

我们看到，外层for循环时间随着n改变，所以是On。内层i每次是指数增长，所以是对数复杂度。所以是NlogN

O n^2

1
2
3
4
5
6
7
8

for(x=1; i<=n; x++)
{
   for(i=1; i<=n; i++)
    {
       j = i;
       j++;
    }
}

俩循环嵌套

空间复杂度

就是看开辟空间了没有。

比如二叉树遍历，如果要记录节点，所以开辟额外空间的空间复杂度是N。递归调用栈深度是树的高度。树的高度是logn因为每一层节点翻倍。

所以如果包含额外空间，则递归调用遍历二叉树节点并储存的话是O N+logN，（N是保存节点，logN是调用栈深度, 保存节点的数量和栈深度没有关联，所以不是nlogn, 而是n+logn）

如果不看这个储存的节点的空间，就是单纯的O logN

堆排序

就是排序一个堆。

最大堆和最小堆只保证父节点比子节点大或者小，他不保证子节点的绝对顺序。

把数据组织成一个最大堆或者最小堆。然后整个堆都是待排序状态。

这时候把堆顶的数（一定是最大的或者是最小的）和最后一个节点的数交换(或者是直接拿出来)。

交换后整个堆的顺序会被破坏，所以需要重新调整以符合最大堆/最小堆定义。然后重复交换-》拿出-》排序的过程。

STL的sort

复合排序

  • 在数据量很大时采用正常的快速排序，此时效率为O(logN)。
  • 一旦分段后的数据量小于某个阈值，就改用插入排序，因为此时这个分段是基本有序的，这时效率可达O(N)。
  • 在递归过程中，如果递归层次过深，分割行为有恶化倾向时，它能够自动侦测出来，使用堆排序来处理，在此情况下，使其效率维持在堆排序的O(N logN)，但这又比一开始使用堆排序好。

https://feihu.me/blog/2014/sgi-std-sort/#stdsort%E9%80%82%E5%90%88%E5%93%AA%E4%BA%9B%E5%AE%B9%E5%99%A8

排序算法稳定性

稳定的算法：

  • 插入排序
  • 冒泡排序
  • 归并排序

快速排序

找到一个pivot，比如数组中间的值。从左往右找，在左边找到第一个比中间的值大的，在右边找到第一个比中间值小的，他俩交换。直到左侧的都比中间值小，右侧的都比中间值大。然后进行递归分别处理左侧的和右侧的。

  • 注意我们写法的递归操作，是start,right 和 left, end。因为我们一定会走到两个下标相等的部分。也就是left = right。也就是刚好处于pivot的位置。然后我们会把left+1， right - 1。这样一来，right就跑到了左边，left就跑到了右边。

unknown (1)

归并排序

归并排序的过程：

  • 必须创建一个额外空间的数组。这也是归并稳定的原因
  • 递归把数组切成两个的大小
  • 然后对这个大小为2的数组进行排序
  • 这个数组排序完成后，对下一个大小为2的数组进行排序
  • 然后对这两个大小为2的数组进行排序
  • …..

具体的排序过程：

  • 我们有我们的额外数组。
  • 在原数组中选择中间值。
  • 使用双指针法，两个指针分别指向第一个元素和中间值后的第一个元素。
  • 如果第一个元素比中间值后的第一个元素大，那么把这个元素放到额外数组。反之亦然。
  • 如果原数组当中的左半部分和右半部分（中间值后面的部分）有未遍历完的，则原样复制到额外数组。
  • 把额外数组的值赋值回原数组。
    • 此处必须格外注意。把额外数组赋值回原数组，起始位置和结束为止是函数的入参。不是从0开始。因为接下来排序整个原数组的后半部分的时候，前半部分已经是相对有序的了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

self.merge_sort(a, 0, 7, temparr)                           |1

        self.merge_sort(a, 0, 3, temparr)  # left               |2
        
            self.merge_sort(a, 0, 1, temparr)  # left               |3
                self.merge_sort(a, 0, 0, temparr)  # left               |4
                self.merge_sort(a, 1, 1, temparr)  # right              |4
                self.sort(a, 0, 1, temparr)  # sort                     |4
                
            self.merge_sort(a, 2, 3, temparr)  # right              |3
                self.merge_sort(a, 2, 2, temparr)  # left               |4
                self.merge_sort(a, 3, 3, temparr)  # right              |4
                self.sort(a, 2, 3, temparr)  # sort                     |4
                
            self.sort(a, 0, 3, temparr)  # sort                     |3
            
        self.merge_sort(a, 4, 7, temparr)  # right              |2
            self.merge_sort(a, 4, 5, temparr)  # left               |3
                self.merge_sort(a, 4, 4, temparr)  # left               |4
                self.merge_sort(a, 5, 5, temparr)  # right              |4
                self.sort(a, 4, 5, temparr)  # sort                     |4
                
            self.merge_sort(a, 6, 7, temparr)  # right              |3
                self.merge_sort(a, 6, 6, temparr)  # left               |4
                self.merge_sort(a, 7, 7, temparr)  # right              |4
                self.sort(a, 6, 7, temparr)  # sort                     |4
                
            self.sort(a, 4, 7, temparr)  # sort                     |3
            
        self.sort(a, 0, 7, temparr)  # sort                     |2

unknown

二分查找

  • left=mid和right=mid不能一起出现在代码里，会死循环
  • left=mid+1和right=mid-1不能一起出现在代码里，会提前跳出

所以left和right的更新就是一个带1一个不带1。取决于mid怎么取整。

  • 如果mid靠right近，则right带1。
  • 如果mid靠left近，则left带1。
  • 靠哪边近的意思是，如果left是4，right是5。如果mid是4那就是left近。

回溯

针对组合问题，没有重复元素，不可取重复的用startindex。 有重复元素且不可取重复的用startindex+used 针对排列问题，不需要startindex。比如全排列。12和21是两种排列。所以不需要startindex。used数组是用来标记同一树枝用过的数字的。 举例：123这个集合，先取了2，因为没有startindex，所以我们还是从1开始取。但是2已经被拿走了，所以2跳过。所以排列问题的used数组去重是判断是否为true。 但是如果排列问题有重复元素，那就是used数组既要判断false也要判断true。也就是树枝和树层都要去重 &树枝去重看used[i] = true 的原因是，我们没有startindex。所以每次都是从开头开始。如果没有树枝去重的话， 112这个组合的第一个1每次都会被选出来。就会出现111这种问题。 所以使用了used[i]可以在一定程度上替代startindex。但是我们不用startindex的原因是，我们从2开始可以选回之前的这个1。因为我们used树枝的限制仅限于单个for循环也就是单个路径。不限制整个路径。 &used树层去重是限制的起始点的值重复。used树枝去重限制的是路径上的选择重复。 for循环控制横向遍历。递归控制纵向遍历。所以我们在for里面操作startindex的时候是改的i而不是startindex。

DP

如果我们是比较类，也就是看放和不放哪个大/小… 的时候，我们会在后面加nums[i] dp[i][j] = max(dp[i-1][j], dp[i-1][j-nums[i]] + nums[i]) 动态规划的核心就是每个物品可以拿也可以不拿。 这里 dp[i-1][j] 的意思是 不拿当前i物品的情况。 这里 dp[i-1][j-nums[i]] + nums[i]的意思是 我要是拿了物品i我就一定得拿。 所以我先把i放进去，把价值加上去这是+nums[i]。 i已经拿了 所以得从i-1看 所以是dp[i-1] 然后算放了i之后我背包还剩下多大，我就找到重量为j-nums[i]时候最大的价值是多少 然后二者取最大值 这个nums[i] 如果是求值那就是这个东西的价值那就是value[i]或者就是nums[i]本身。如果是求个数 那就是+1

如果是累加类 也就是求组合类 求有多少种组合或者方法 比如 518 和 494 那就不加nums[i] 二维不要用+= 还是按照+的老方法 例子： dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i]] 这里 dp[i-1][j] 是我如果不拿的情况 dp[i-1][j-nums[i]] 的意思是 i已经拿了 所以得从i-1看 所以是dp[i-1] 然后我因为是求方法数量 不需要具体nums[i]的数值。所以没有+nums[i] 但是我依旧还是看当我一定要装i的时候，装了i之后背包还剩多大。我要去看重量为j-nums[i]的时候的最大值是多少。然后相加就可以

防止加法溢出

int mid = (left + right) / 2

替换为

int mid = left + (right - left) / 2

二叉树

二叉搜索树

  • 二叉搜索树的中序遍历是有序的
  • 二叉搜索树的左子树上所有结点的值均小于它的根结点的值以及右子树上所有结点的值均大于它的根结点的值
  • 在最好的情况下，二叉搜索树的查找效率比较高，是 O(logn)，其访问性能近似于二分法；
  • 但最差时候会是 O(n)，比如插入的元素是有序的，生成的二叉搜索树就退化为一个链表，树的一条腿特变长，这种情况下，需要遍历全部元素才行

完全二叉树

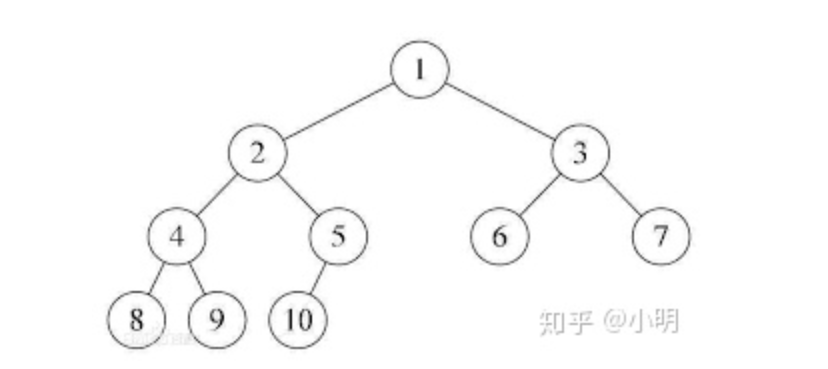
看到完全二叉树可以想成一个堆。

如果给的输入是二叉树的层序遍历，则 对于任意节点,

  • 若其下标为i 则父节点下标k为 i/2 - (i%2 == 0 ? 1 : 0);
  • 若当前为i, 两个子节点下标为 i*2 + 1 和i*2+2

满二叉树

  • 节点全满的就是满二叉树

QQ截图20221026185828

完全二叉树

  • 完全二叉树由满二叉树转化而来，也就是将满二叉树从最后一个节点开始删除，一个一个从后往前删除，剩下的就是完全二叉树。

QQ截图20221026185832

前缀和

如果想知道nums[i] ~ nums[j] 的和，我们只需要计算presum[j+1] - presum[i] 即可

比如

1
2

nums = 	   [1,2,3,4, 5, 6, 7]
presum = [0,1,3,6,10,15,21,28]

假如我们想知道nums[2] ~ nums[5]的和，也就是3+4+5+6 = 19

我们可以通过计算presum[5+1] - presum[2] = 21 - 3 = 19

加1是因为前缀和比原数组在开头多一个0。

注意区分开差分数组和前缀和的区别。

我们假设新的例子

1
2
3

nums =		  [1,2,4,6, 7, 20,10,3];
diff = 	     [1,1,2,2, 1, 13,-10,-7];
presum = 	[0,1,3,7,13,20,40,50,53];

前缀和怎么算的？

1
2
3
4
5
6
7
8

accumu = accumu + nums[i-1];
presum[i] = accumu; 或
presum[i] = presum[i - 1] + nums[i - 1] 因为有前导0
0+1=1
1+2=3
3+4=7
7+6=13
...

差分数组怎么算的？

1
2
3
4
5
6
7

nums[i] - nums[i - 1] = diff[i]
1-0 = 1（虚拟0）
2-1 = 1
4-2 = 2
6-4 = 2
7-6 = 1
...

字典树

字典树的节点有两个东西。一个是is_word用来判断到这个节点位置是否可以组成一个单词

第二个是储存下一层节点的指针的容器。二叉树只有左右两个，而字典树最坏情况每一个节点都会有26个。

针对区间和类问题选择合适方法

针对不同的题目，我们有不同的方案可以选择（假设我们有一个数组）：

  • 数组不变，求区间和：「前缀和」、「树状数组」、「线段树」
  • 多次修改某个数（单点），求区间和：「树状数组」、「线段树」
  • 多次修改某个区间，输出最终结果：「差分」
  • 多次修改某个区间，求区间和：「线段树」、「树状数组」（看修改区间范围大小）
  • 多次将某个区间变成同一个数，求区间和：「线段树」、「树状数组」（看修改区间范围大小）
  1. 简单求区间和，用「前缀和」
  2. 多次将某个区间变成同一个数，用「线段树」
  3. 其他情况，用「树状数组」

https://leetcode.cn/problems/range-sum-query-mutable/solution/guan-yu-ge-lei-qu-jian-he-wen-ti-ru-he-x-41hv/

笔记
C++
本文由作者按照 CC BY 4.0 进行授权
最近更新
文章内容